Ngược dòng lịch sử: Vì sao bắt học sinh phải giải phương trình bậc 2 trong khi không cần thiết?
Kiến thức - Học thuật - Ngày đăng : 11:28, 30/12/2022
Giải phương trình bậc hai
Đại số thậm chí là gì? Bạn có thể nghĩ về nó - hoàn toàn chính đáng, dựa trên cách nó được dạy theo truyền thống - như một mê cung đáng sợ của các phương trình, một hỗn hợp bảng chữ cái x, y, z, a, b và c, cộng với một số mũ (2 và 3 và có thể là 4). Đối với những người không quen biết, nó chắc chắn gây khó chịu. Nhưng không có lý do gì mà đại số lại có vấn đề. Nó thực sự chỉ là nghệ thuật khám phá ẩn số bằng cách sử dụng dữ liệu chúng ta biết.
Tên của "đại số" tiếng Anh là algebra xuất phát từ từ al-jabr trong tên gọi cuốn sách của Muhammad al-Khwarizmi vào thế kỷ thứ 9. Cuốn sách tập hợp các ý tưởng của người Ai Cập, Babylon, Hy Lạp, Trung Quốc và Ấn Độ về việc tìm các số chưa biết, dựa trên một số dữ liệu khác. Al-Khwarizmi cung cấp cho chúng ta các phương pháp - các công thức mà chúng ta gọi là thuật toán - để giải các phương trình đại số cơ bản như ax2 + bx = c, và các phương pháp hình học để giải 14 loại phương trình "lập phương" khác nhau (trong đó x được nâng lên lũy thừa 3) .
Tại thời điểm này trong lịch sử, người ta không gọi ẩn số là x, cũng không có bất kỳ thứ gì thực sự được nâng lên lũy thừa, cũng như không có bất kỳ phương trình nào trong những gì al Khwarizmi đã viết. Đại số ban đầu là "hùng biện", sử dụng một mớ từ ngữ phức tạp để đặt ra một vấn đề và để giải thích giải pháp. Ẩn số được tìm kiếm thường được gọi là cossa, hay "sự vật", và vì vậy đại số thường được gọi là "Nghệ thuật Cossick" - Nghệ thuật của sự vật. Một sinh viên đầu tiên của Nghệ thuật Cossick có thể thấy mình phải đối mặt với những thứ gọi là bài toán kiểu như thế này:
“Hai người đàn ông đang dắt đàn bò của họ dọc theo một con đường, và một người nói với người kia: “Hãy cho tôi hai con bò, tôi sẽ số bò giống như anh”. Người kia nói: “Bây giờ anh cho tôi hai con bò, tôi sẽ được gấp đôi số anh có”. Vậy có bao nhiêu con bò ở đó và mỗi người có bao nhiêu con?”.
hoặc
“Tôi có một tấm vải lanh dài 60 mét và rộng 40 mét. Tôi muốn cắt nó thành nhiều phần nhỏ hơn, mỗi phần có chiều dài 6 mét, chiều rộng 4 mét, để mỗi phần đủ lớn để làm một chiếc áo dài. Có bao nhiêu chiếc áo chẽn có thể được làm từ một tấm vải lanh?”.
Những ví dụ này đã được Alcuin ở York thu thập vào khoảng năm 800 sau Công nguyên, và được xuất bản trong một bản tóm tắt các câu đố có tên là "Vấn đề rèn giũa giới trẻ". Chúng không khác mấy so với những câu hỏi mà chúng ta phải đối mặt trong các bài học toán ở trường. Tuy nhiên, chúng ta có lợi thế là có thể biến chúng thành phương trình và khái quát vấn đề một cách dễ dàng.
Chỉ đến thế kỷ 16, người ta mới nghĩ đến việc loại bỏ việc diễn giải đại số bằng lời nói. Ý tưởng đến với một công chức người Pháp tên là Francois Viete. Sau khi được đào tạo thành luật sư, Viete đã dành phần lớn sự nghiệp của mình để phục vụ cho triều đình Pháp. Ông là một quản trị viên ở Brittany, một cố vấn bí mật của hoàng gia cho vua Henry III, và là người giải mật cho vua Henry IV. Khoảnh khắc đáng tự hào nhất của Viete có lẽ đã đến khi vua Tây Ban Nha buộc tội tòa án Pháp về dùng ma thuật bùa chú. Vua Tây Ban Nha tố với Giáo hoàng rằng Pháp làm sao có thể biết trước về các kế hoạch quân sự của Tây Ban Nha nếu không dùng ma thuật? Nhưng tất nhiên không có phép thuật nào cả. Viete đơn giản là thông minh hơn những người viết mật mã Tây Ban Nha và đã có thể giải mã thông tin liên lạc của họ khi mật mã bị lính Pháp chặn lại.
Có lẽ chính sự nhanh nhạy về trí óc này đã giúp Viete thấy rằng ẩn dụ trong đại số sẽ dễ dàng hơn nếu nó được mã hóa thành các ký hiệu. Trong môn đại số của mình, Viete đã sử dụng phụ âm để chỉ định các tham số và nguyên âm cho các ẩn số. Ông ấy sẽ viết một cái gì đó như kiểu như là:
A lập phương + B bình phương x A = B bình phương x Z (còn chúng ta bây giờ đơn giản viết là: A3 + B2A = B2Z).
Cách thể hiện phương trình của Viete vẫn khá là cồng kềnh nhưng vạn sự khởi đầu nan mà. Thật thú vị khi biết rằng dấu cộng (+) đã xuất hiện ở đây (và dấu trừ (-) cũng có trong thời gian này, nhưng dấu (=) thì chưa xuất hiện. Nhà toán học xứ Wales Robert Recorde đã lần đầu tiên giới thiệu dấu bằng vào năm 1557. Cũng trong thời này, ẩn số x chưa hề xuất hiện.
Lý do chữ "x" được dùng biểu thị cho ẩn số vẫn còn đang bị tranh cãi gay gắt. Theo nhà sử học văn hóa Terry Moore, đó là vì đại số ban đầu của al-Khwarizmi đã sử dụng al-shay-un có nghĩa là "điều không xác định". Khi các dịch giả tiếng Tây Ban Nha thời trung cổ đang tìm kiếm một từ tương đương trong tiếng Latinh, họ đã sử dụng từ gần nhất mà họ có với từ "sh", vốn không thực sự tồn tại trong tiếng Tây Ban Nha. Và thế là chúng ta đã kết thúc với chữ cái tạo ra âm "ch" trong tiếng Tây Ban Nha: x.
Nhưng các nguồn khác nói rằng đó là do René Descartes, người chỉ đơn giản là đưa hai thái cực của bảng chữ cái vào hoạt động trong cuốn sách La Geometrie năm 1637 của ông. Ông đã khái quát hóa các tham số đã biết thành a, b và c; các ẩn số được chỉ định x, y và z.
Nếu bạn phát mệt về đại số, với tất cả các ký hiệu bí ẩn của nó, thì bạn có thể nghĩ về nó như một cách chuyển các hình dạng hình học thành dạng viết.
Đại số để phục vụ hình học
Chúng ta thường học đại số và hình học dưới dạng các chủ đề riêng biệt vì chủ yếu là vì nó giúp thiết kế chương trình giảng dạy ở trường dễ dàng hơn. Nhưng thực sự đại số chảy liền mạch từ hình học; đó là hình học được thực hiện mà không cần hình ảnh, một động thái giải phóng nó và cho phép toán học phát triển. Để xem làm thế nào, chúng ta hãy quay trở lại với các thông lệ đánh thuế cổ xưa.
Như chúng ta đã thấy khi xem xét hình học, thuế thường dựa trên diện tích ruộng - từ tiếng Babylon có nghĩa là diện tích, eqlum, ban đầu có nghĩa là "ruộng". Không có gì ngạc nhiên khi các nhà quản lý Babylon phải học cách giải các câu đố như câu đố này được đưa ra trên tấm bảng Babylon cổ đại YBC 6967, nằm trong bộ sưu tập của Yale:
Diện tích hình chữ nhật là 60 và chiều dài hơn chiều rộng 7. Chiều rộng là bao nhiêu?
Hãy thử giải quyết nó. Nếu chiều rộng là x, chiều dài là x + 7. Diện tích hình chữ nhật chỉ đơn giản là chiều rộng nhân với chiều dài, vì vậy diện tích A được cho bởi phương trình sau:
A = x(x + 7).
Dấu ngoặc đơn ở đây yêu cầu bạn nhân từng số hạng bên trong ngoặc đơn với số ngay bên ngoài nó, điều này dẫn đến:
A = x2 + 7x
Người Babylon sẽ giải quyết vấn đề này thông qua một loạt các bước minh họa mối liên hệ chặt chẽ giữa đại số và hình học. Quá trình này được gọi là "hoàn thành hình vuông".
Để làm cho một phương trình loại x2 + bx có thể quản lý được, trước tiên bạn vẽ nó dưới dạng các hình dạng hình học. x2 chỉ là bình phương của cạnh x. bx là hình chữ nhật có chiều dài x và chiều rộng b. Chia hình chữ nhật đó thành hai chiều dài và di chuyển một nửa xuống dưới cùng của hình vuông ban đầu, và bạn gần như có thể tạo một hình vuông lớn hơn. Để hoàn thành hình vuông lớn hơn đó, bạn chỉ cần thêm vào một hình vuông nhỏ cạnh b/2. Diện tích của hình vuông nhỏ này là (b/2)2. Vì vậy, bạn có thể thấy rằng biểu thức ban đầu thực sự tương đương với (x + b/2)2 – (b/2)2.
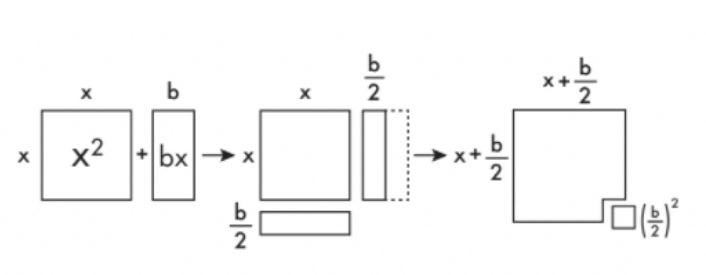
Cho một phương trình có dạng
x2 + bx = c
người Babylon sẽ thay thế trong kết quả hoàn thành hình vuông, làm cho nó:
(x + b/2)2 – (b/2)2 = c
Sau đó, họ sẽ giải quyết vấn đề này và rút gọn tất cả thành công thức (mặc dù nó không được viết dưới dạng công thức theo nghĩa hiện đại):
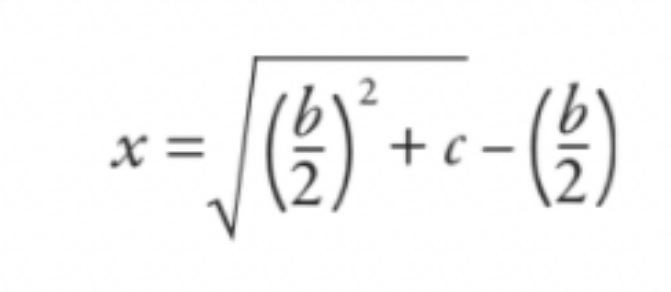
Câu trả lời là chiều rộng là 5 và chiều dài là 12. Nhưng chúng ta tự hỏi liệu công thức đó có hơi quen thuộc không? Nếu cung cấp cho bạn một tinh chỉnh đối với phương trình ban đầu để bạn có
ax2 + bx + c = 0
bạn sẽ giải bài toán này bằng công thức đã học ở trường - công thức giải phương trình bậc hai.
Như bạn có thể thấy rõ ràng, những gì bạn học được ở trường không hơn gì một công cụ tính thuế 5.000 năm tuổi. Tuy nhiên, không ai trong chúng ta lớn lên trở thành quan chức thuế của Babylon, vậy tại sao ngày nay học sinh lại học công thức bậc hai? Đó là một câu hỏi gây tranh cãi ngay cả giữa các giáo viên dạy toán.
